Explicit Formula For Geometric Sequence

Calculate anything and everything about a geometric progression with our geometric sequence calculator. This geometric series figurer volition assist y'all empathize the geometric sequence definition, so you could answer the question, what is a geometric sequence?

We explain the difference betwixt both geometric sequence equations, the explicit and recursive formula for a geometric sequence, and how to apply the geometric sequence formula with some interesting geometric sequence examples.

We as well accept congenital a "geometric series computer" function that will evaluate the sum of a geometric sequence starting from the explicit formula for a geometric sequence and building, pace by step, towards the geometric serial formula.

Geometric sequence definition

The geometric sequence definition is that a collection of numbers, in which all simply the first one, are obtained by multiplying the previous one past a fixed, non-zero number called the common ratio. If you are struggling to sympathise what a geometric sequences is, don't fret! We will explain what this means in more than simple terms later on, and take a look at the recursive and explicit formula for a geometric sequence. We also include a couple of geometric sequence examples.

Before we dissect the definition properly, information technology's of import to clarify a few things to avert defoliation. First of all, we demand to sympathize that even though the geometric progression is fabricated upward by constantly multiplying numbers by a factor, this is non related to the factorial. Indeed, what it is related to is the greatest mutual factor (GFC) and everyman common multiplier (LCM) since all the numbers share a GCF or a LCM if the first number is an integer.

This means that the GCF is simply the smallest number in the sequence. Conversely, the LCM is simply the biggest of the numbers in the sequence. For example, in the sequence iii, 6, 12, 24, 48 the GCF is 3 and the LCM would be 48. Merely if we consider only the numbers 6, 12, 24 the GCF would exist 6 and the LCM would be 24.

Geometric progression: What is a geometric progression?

At present permit'south meet what is a geometric sequence in layperson terms. A geometric sequence is a collection of specific numbers that are related by the common ratio we have mentioned earlier. This common ratio is i of the defining features of a given sequence, together with the initial term of a sequence. Nosotros volition come across after how these two numbers are at the basis of the geometric sequence definition and depending on how they are used, one tin can obtain the explicit formula for a geometric sequence or the equivalent recursive formula for the geometric sequence.

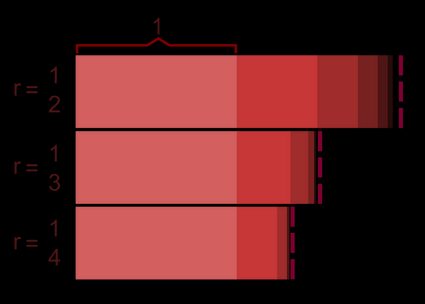
Geometric sequence examples with different ratios

Now, let's construct a unproblematic geometric sequence using physical values for these two defining parameters. To make things simple, we will have the initial term to be 1 and the ratio will be prepare to 2. In this instance, the start term will exist a₁ = 1 by definition, the 2nd term would be a₂ = a₁ * 2 = 2, the third term would and so exist a₃ = a₂ * two = iv etc. The n-th term of the progression would then be:

aₙ = 1 * 2ⁿ⁻¹,

where due north is the position of said term in the sequence.

As you can see, the ratio of whatsoever two consecutive terms of the sequence - defined merely like in our ratio calculator - is constant and equal to the common ratio.

A common mode to write a geometric progression is to explicitly write down the first terms. This allows you to calculate any other number in the sequence; for our example, we would write the series every bit:

1, ii, 4, viii, ...

Even so, there are more mathematical ways to provide the same information. These other ways are the and then-called explicit and recursive formula for geometric sequences. Now that we sympathise what is a geometric sequence, nosotros can dive deeper into this formula and explore ways of conveying the same information in fewer words and with greater precision.

Recursive vs. explicit formula for geometric sequence.

There exist two distinct ways in which you lot tin mathematically represent a geometric sequence with just i formula: the explicit formula for a geometric sequence and the recursive formula for a geometric sequence. The offset of these is the one nosotros have already seen in our geometric series example. What we saw was the specific explicit formula for that example, but you can write a formula that is valid for any geometric progression – you can substitute the values of a₁ for the corresponding initial term and r for the ratio. The general formula for the n-th term is:

aₙ = a₁ * rⁿ⁻¹ north ∈ 𝗡 ,

where n ∈ 𝗡 ways that north = 1, 2, 3, .... The recursive formula for geometric sequences conveys the most of import information virtually a geometric progression: the initial term a₁, how to obtain any term from the beginning one, and the fact that there is no term earlier the initial.

There is another manner to prove the same information using another type of formula: the recursive formula for a geometric sequence. It is made of two parts that convey different data from the geometric sequence definition. The kickoff office explains how to get from any fellow member of the sequence to whatsoever other member using the ratio. This significant alone is not plenty to construct a geometric sequence from scratch, since we do non know the starting point. This is the second office of the formula, the initial term (or any other term for that affair). Permit's see how this recursive formula looks:

aₙ = aₙ₋₁ * r aᵢ = x

Where x is used to express the fact that any number volition be used in its place, but also that it must be an explicit number and not a formula. The subscript i indicates any natural number (but like n) only it'south used instead of n to get in clear that i doesn't need to be the same number equally n.

How to utilize the geometric sequence calculator?

Now that you know what a geometric sequence is and how to write 1 in both the recursive and explicit formula, it is fourth dimension to apply your cognition and calculate some stuff! With our geometric sequence calculator, you tin can calculate the most of import values of a finite geometric sequence. These values include the mutual ratio, the initial term, the last term and the number of terms. Hither's a brief description of them:

Initial term — First term of the sequence.
Common ration — Ratio between the term aₙ and the term aₙ₋₁.
Number of terms — How many numbers does your geometric sequence contain?.
north-th term — Value of the terminal term.
Sum of the first N terms — Issue of adding up all the terms in the finite series.
Infinite sum — Sum of all terms possible, from n=1 to n=∞.

These terms in the geometric sequence calculator are all known to us already, except the terminal ii, nearly which we will talk in the post-obit sections. If you ignore the summation components of the geometric sequence figurer, you lot just need to introduce whatsoever three of the 4 values to obtain the fourth element. The sums are automatically calculated from these values; but seriously, don't worry about information technology besides much, we volition explain what they hateful and how to employ them in the next sections.

Geometric series formula: the sum of a geometric sequence

So far we have talked near geometric sequences or geometric progressions, which are collections of numbers. However, there are actually interesting results to be obtained when you lot try to sum the terms of a geometric sequence. When we accept a finite geometric progression, which has a express number of terms, the process hither is as unproblematic equally finding the sum of a linear number sequence. Calculating the sum of this geometric sequence tin fifty-fifty be done by hand, theoretically.

Just we can exist more efficient than that past using the geometric serial formula and playing around with it. To practise this we will use the mathematical sign of summation (∑) which means summing up every term after it. For case, if we have a geometric progression named Pₙ and we name the sum of the geometric sequence Southward, the relationship between both would be:

Due south = ∑ Pₙ

While this is the simplest geometric series formula, information technology is too not how a mathematician would write information technology. In mathematics, geometric series and geometric sequences are typically denoted but by their full general term aₙ, so the geometric serial formula would look similar this:

Southward = ∑ aₙ = a₁ + a₂ + a₃ + ... + aₘ

where m is the total number of terms we want to sum.

Unfortunately, this still leaves you with the trouble of really calculating the value of the geometric series. You could e'er use this calculator as a geometric serial reckoner, but it would be much better if, earlier using any geometric sum estimator, you understood how to practise information technology manually. In that location is a trick that tin can make our job much easier and involves tweaking and solving the geometric sequence equation similar this:

S = ∑ aₙ = ∑ a₁rⁿ⁻¹ = a₁ + a₁r + a₁r² + ... + a₁rᵐ⁻¹

Now multiply both sides past (1-r) and solve:

S * (1-r) = (1-r) * (a₁ + a₁r + a₁r² + ... + a₁rᵐ⁻¹)

S * (1-r) = a₁ + a₁r + ... + a₁rᵐ⁻¹ - a₁r - a₁r² - ... - a₁rᵐ = a₁ - a₁rᵐ

S = ∑ aₙ = a₁ - a₁rᵐ / (1-r)

This result is i you can easily compute on your own, and information technology represents the bones geometric serial formula when the number of terms in the series is finite. However, this is math and not the Real Life™ so we tin can actually have an infinite number of terms in our geometric series and nonetheless exist able to calculate the total sum of all the terms. How does this wizardry work? – I hear you lot ask. Well, fearfulness not, we shall explain all the details to you, young apprentice.

Using the geometric sequence formula to calculate the infinite sum

After seeing how to obtain the geometric series formula for a finite number of terms, it is natural (at least for mathematicians) to ask how can I compute the infinite sum of a geometric sequence? Information technology might seem impossible to do so, but certain tricks let usa to calculate this value in a few uncomplicated steps. For this, we demand to introduce the concept of limit. This is a mathematical process by which nosotros tin understand what happens at infinity. It can as well be used to try to define mathematically expressions that are commonly undefined, such every bit nix divided past zero or cypher to the ability of zero.

Talking almost limits is a very circuitous bailiwick, and it goes beyond the scope of this calculator. Their complexity is the reason that we take decided to just mention them, and to non go into detail most how to calculate them. Do not worry though considering you can find first-class information in the Wikipedia article nearly limits.

Even if you tin can't be bothered to bank check what the limits are, you tin still calculate the infinite sum of a geometric serial using our reckoner. The just matter you need to know is that not every series has a defined sum. The conditions that a series has to fulfill for its sum to be a number (this is what mathematicians call convergence), are, in principle, unproblematic. Nosotros explain them in the following section.

When it comes to mathematical serial (both geometric and arithmetics sequences), they are often grouped in two dissimilar categories, depending on whether their space sum is finite (convergent series) or space / non-divers (divergent series). The best fashion to know if a serial is convergent or not is to summate their space sum using limits. Short of that, there are some tricks that can allow u.s. to rapidly distinguish between convergent and divergent series without having to practise all the calculations. These tricks include: looking at the initial and full general term, looking at the ratio, or comparing with other series.

Visualization of the sum of a geometrical sequence

For a serial to be convergent, the full general term (aₙ) has to get smaller for each increase in the value of n. If aₙ gets smaller, we cannot guarantee that the series will exist convergent, but if aₙ is constant or gets bigger as nosotros increase north we can definitely say that the series will be divergent. If we are not certain whether aₙ gets smaller or non, we can simply expect at the initial term and the ratio, or fifty-fifty calculate some of the first terms. This will give united states of america a sense of how aₙ evolves.

The second choice we take is to compare the evolution of our geometric progression against one that we know for certain converges (or diverges), which can be done with a quick search online. Speaking broadly, if the serial nosotros are investigating is smaller (i.due east., aₙ is smaller) than one that we know for sure that converges, we can be sure that our series will besides converge. Conversely, if our series is bigger than i nosotros know for sure is divergent, our serial will always diverge. In the residuum of the cases (bigger than a convergent or smaller than a divergent) we cannot say anything about our geometric series, and we are forced to detect some other serial to compare to or to utilize some other method.

These criteria apply for arithmetic and geometric progressions. In fact, these two are closely related with each other and both sequences tin exist linked by the operations of exponentiation and taking logarithms.

Zeno'southward paradox and other geometric sequence examples

Nosotros have already seen a geometric sequence example in the grade of the so-called Sequence of powers of two. This is a very important sequence because of computers and their binary representation of information. In this progression, we tin can find values such as the maximum immune number in a computer (varies depending on the blazon of variable we use), the numbers of bytes in a gigabyte, or the number of seconds till the end of UNIX time (both original and patched values).

On superlative of the power-of-two sequence, we can have any other power sequence if nosotros merely supervene upon r = 2 with the value of the base of operations nosotros are interested in. Power series are commonly used and widely known and can be expressed using the convenient geometric sequence formula. But this power sequences of any kind are not the but sequences we can have, and nosotros will bear witness you even more of import or interesting geometric progressions similar the alternating serial or the mind-blowing Zeno's paradox.

Let'southward kickoff with Zeno's paradoxes, in particular, the then-chosen Dichotomy paradox. This paradox is at its core but a mathematical puzzle in the form of an infinite geometric series. Zeno was a Greek philosopher that pre-dated Socrates. He devised a mechanism by which he could prove that motion was impossible and should never happen in existent life. The idea is to divide the distance between the starting signal (A) and the finishing bespeak (B) in half. In one case you take covered the kickoff half, you divide the remaining distance half once again… You can echo this process as many times equally you lot want, which means that you volition always accept some distance left to become to point B.

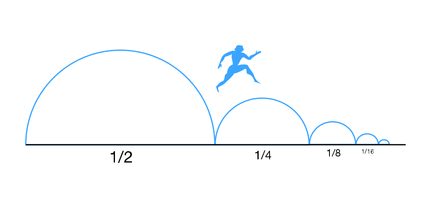
Zeno's paradox seems to predict that, since nosotros take an infinite number of halves to walk, nosotros would demand an infinite corporeality of time to travel from A to B. However, as we know from our everyday experience this is not true, and we tin always get to point A to point B in a finite corporeality of time (except for Spanish people that ever seem to arrive infinitely late everywhere). The solution to this credible paradox can be constitute using math.

If we express the fourth dimension it takes to get from A to B (permit's phone call it t for now) in the course of a geometric series, we would take a serial defined by: a₁ = t/ii with the common ratio being r = 2. So the first half would have t/2 to be walked, then nosotros would cover half of the remaining altitude in t/4, then t/viii, etc… If we now perform the infinite sum of the geometric series, we would find that:

S = ∑ aₙ = t/2 + t/four + ... = t * (1/2 + one/4 + 1/8 + ...) = t * i = t

This is the mathematical proof that we tin become from A to B in a finite amount of time (t in this instance).

To finish it off, and in example Zeno'south paradox was not enough of a mind-blowing experience, permit'southward mention the alternating unit series.
This series starts at a₁ = one and has a ratio r = -1 which yields a serial of the class:

Southward = ∑ aₙ = i - 1 + ane - 1 + ...

Which does not converge according to the standard criteria because the result depends on whether we take an even (Due south = 0) or odd (Due south = i) number of terms. At that place is a pull a fast one on by which, however, we can "make" this series converges to one finite number. The trick itself is very simple, just it is cemented on very complex mathematical (and even meta-mathematical) arguments, so if you ever evidence this to a mathematician yous risk getting into big trouble. You've been warned. Allow's see the "solution":

Due south = ane - 1 + 1 - 1 + ...

We multiply both sides by -1:

-South = -1 + 1 - 1 + one - ... = -1 + (one - 1 + one - ane + ...) = -i + Southward

If we solve for South at present:

-S - Southward = -1 → 2S = 1 → S = 1/2

At present you can go and show-off to your friends, every bit long as they are not mathematicians.

FAQ

What is the geometric sequence?

A geometric sequence is a series of numbers such that the side by side term is obtained by multiplying the previous term by a common number.

How to notice the sum of a geometric sequence?

To find the sum of a geometric sequence:

Summate the common ratio, r raised to the power n.
Subtract the resultant rⁿ from 1.
Divide the resultant by (1 - r).
Multiply the resultant by the first term, a₁ .

How to find the nth term of a geometric sequence?

To discover the nth term of a geometric sequence:

Calculate the common ratio raised to the ability (northward-1).
Multiply the resultant by the first term, a.

How to summate the common ratio of a geometric sequence?

To summate the common ratio of a geometric sequence, divide whatever 2 consecutive terms of the sequence.